I wrote this ML challenge for this year's UMDCTF competition. It's a fun \(L_0\)-constrained adversarial attack problem.
the fremen are trying to sabotage the spice harvest and they need your help! spice harvesters have worm
image recognition technology to know when to avoid a worm attack. luckily for you, a hacker genius got access
to the pixels of the worm image, but you can only change up to 30 pixels of it. can you help the
fremen destroy a spice harvester?We are provided model.pt storing model weights, server.py, and an image of a worm.

#!/usr/local/bin/python
import sys
import numpy as np
from PIL import Image
import torch
import torch.nn as nn
from torchvision.models import resnet18
model = resnet18()
model.fc = nn.Linear(model.fc.in_features, 1)
model.load_state_dict(torch.load('model.pt'))
original = np.array(Image.open("worm.png"))
modified = original.copy()
inp = input(f"Enter a list of pixels to change, in the format 'x,y,r,g,b;x,y,r,g,b;...':\n")
try:
pixels = inp.split(";")
assert len(pixels) <= 30
for pixel in pixels:
x, y, r, g, b = map(int, pixel.split(","))
modified[y, x] = [r, g, b]
except:
print("Too many pixel changes.")
sys.exit(0)
x = torch.tensor(modified.transpose(2, 0, 1) / 255.0, dtype=torch.float32).unsqueeze(0)
with torch.no_grad():
y = torch.sigmoid(model(x))
if y >= 0.5:
print("that's clearly a worm buddy")
sys.exit(0)
with open("flag.txt", "r") as f:
print("LISAN AL GAIB")
print(f.read())
As with many of my adversarial ML challenges, we are given a ResNet model performing binary image classification. We are asked to submit an image which satisfies two constraints: that there are at most 30 pixels changed and that the image is not classified as a worm.
The first observation to make is that this constraint on number of pixels changed is technically an \(L_0\) constraint. \(L_0\) is a "norm" (not technically a norm - it doesn't satisfy the triangle inequality) that measures the number of non-zero elements in a vector. We basically have that \(\|x_1-x_2\|_0\leq 30\).
If you look into adversarial attacks under \(L_0\) constraint, you'll find a number of options. I had recently read this paper https://arxiv.org/abs/2402.01879 which inspired me to make this challenge, so I implemented my solve based on their method.
My solve script is below. I will talk through some of the details, though I also tried to comment it thoroughly.
import math
import torch
from torch import nn
from torchvision.models import resnet18
import torchvision.transforms as T
from PIL import Image
# load model
model = resnet18()
model.fc = nn.Linear(model.fc.in_features, 1)
model.load_state_dict(torch.load("model.pt"))
# load worm
worm = Image.open("worm.png")
worm = T.ToTensor()(worm).unsqueeze(0)
int_worm = (worm * 255).int()
# initialize perturbation
d = torch.zeros_like(worm, requires_grad=True)
# define number of optimization steps
num_steps = 25000
# define loss function and optimizer
criterion = nn.BCEWithLogitsLoss()
optim = torch.optim.Adam([d], lr=1.0)
# initialize best adversarial perturbation
best_adv_l0 = worm[0, 0].numel()
best_adv = worm.clone()
# initialize sparsity threshold
t = torch.tensor(0.3)
# perform optimization
for i in range(num_steps):
# compute adversarial image
adv_worm = worm + d
# compute classification loss
logits = model(adv_worm)
bce_loss = criterion(logits, torch.tensor([[1.]]))
# save best adversarial perturbation
is_adv = (logits < 0).squeeze()
new_l0 = torch.count_nonzero(((adv_worm * 255).int() - int_worm).abs().sum(dim=1)).item()
if is_adv and new_l0 < best_adv_l0:
best_adv_l0 = new_l0
best_adv = adv_worm.detach().clone()
# compute full loss including L_0 norm approximation
# I also tried the below commented pixelwise L_0 approximation,
# but it didn't work as well despite being what I'm really trying to obtain
# l0_approx_normalized = (d.square() / (d.square() + 0.001)).sum(dim=1).clamp(0, 1).mean()
l0_approx_normalized = (d.square() / (d.square() + 0.001)).mean()
adv_loss = (-bce_loss + l0_approx_normalized)
# compute gradient
optim.zero_grad()
adv_loss.backward()
# normalize gradient with respect to L_inf norm
d_grad_inf_norm = d.grad.norm(p=float("inf")).clamp_(min=1e-12)
d.grad.div_(d_grad_inf_norm)
# update perturbation
optim.step()
# clamp perturbation such that the resulting image is between 0 and 1
d.data.add_(worm).clamp_(0, 1).sub_(worm)
# adjust learning rate according to cosine annealing schedule
n = 0.1 + 0.9 * (1 + math.cos(math.pi * i / num_steps)) / 2
optim.param_groups[0]['lr'] = n
# adjust sparsity threshold
# if the adversarial image is misclassified, increase the threshold to encourage sparsity
# if the adversarial image is classified correctly, decrease the threshold to encourage misclassification
t.add_(torch.where(is_adv, 0.01 * n, -0.01 * n)).clamp_(0, 1)
# filter components by sparsity threshold
d.data[d.data.abs() < t] = 0
# define pixel tensors for original image and adversarial image
out = (best_adv * 255).int().squeeze().transpose(0, 1).transpose(1, 2)
worm = int_worm.squeeze().transpose(0, 1).transpose(1, 2)
# save adversarial image so we can look at it
Image.fromarray(out.numpy().astype("uint8")).save("out.png")
# print the adversarial image in the format expected by the server
changed_px = torch.nonzero((out - worm).abs().sum(dim=2))
out_str = ";".join([f"{x},{y},{','.join(map(str, out[y, x].tolist()))}" for y, x in changed_px])
print(out_str)
print(len(changed_px))The attack uses a couple neat tricks to ensure we don't change too many pixels.
For one, we maintain a sparsity threshold while performing our optimization of the image. After the updates to the image at each iteration, we adjust the sparsity threshold depending on whether the image was classified correctly or not. The idea is that if the image is misclassified, we have achieved our goal, and therefore we might be able to make our adversarial change even more sparse. However, if the image was classified correctly, we probably have to change more pixels in order to obtain a misclassification, and hence we lower the sparsity threshold. After the update to the sparsity threshold, we modify our adversarial delta by setting every component less than our threshold to 0, ensuring a sparse change.
Another neat trick is utilizing a differentiable approximation of the \(L_0\) norm in our loss function. We intend to minimize the \(L_0\) while maximizing the classification loss, so our overall loss is -bce_loss + l0_approx_normalized. This \(L_0\) approximation is pretty interesting. Below is a graph of the approximation:
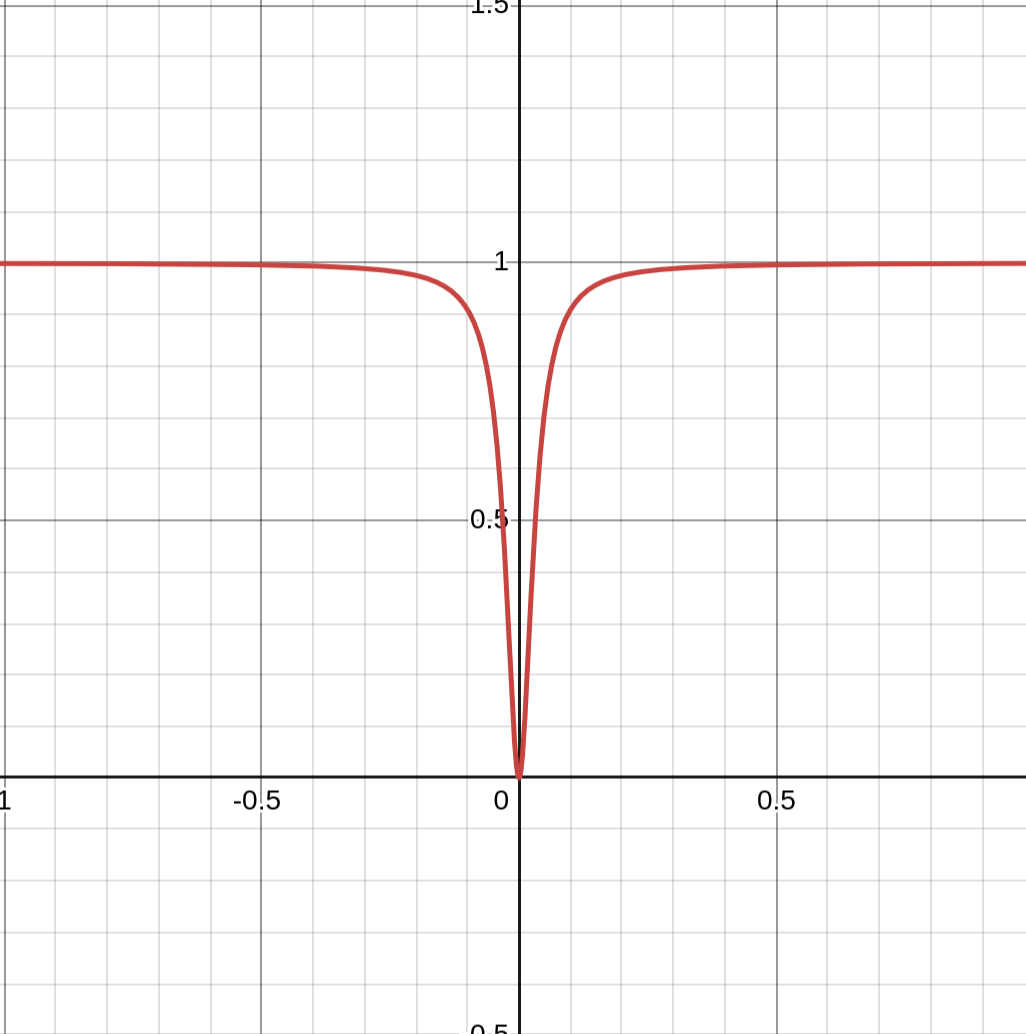
You can see that it's a smooth approximation for a function that is 0 when the input is 0 and 1 otherwise, exactly as the \(L_0\) should be. Choosing a smaller epsilon factor than 0.001 yields a sharper curve, but I found 0.001 to be effective.
There's a couple other little things like using a cosine annealing schedule for learning rate adjustment and gradient normalization, but these are more general optimization techniques moreso than interesting \(L_0\) tricks.
Here's an adversarial example:

We ultimately get the flag: UMDCTF{spice_harvester_destroyed_sunglasses_emoji}. This challenge got 11 solves during the competition. Challenge source is available here: https://github.com/UMD-CSEC/UMDCTF-2024-Challenges/tree/main/misc/attack-of-the-worm